【計算理論】有限オートマトン

オートマトンとは

オートマトンは、特定の文字列を認識する、状態や遷移をモデル化したものです。

この記事では、オートマトンの中の有限オートマトンについて解説していきます。

有限オートマトンとは、名前の通り有限個の状態と遷移からなるオートマトンのことです。

実際に有限オートマトン$M_1$の状態遷移図を書いてみると以下のようになります。

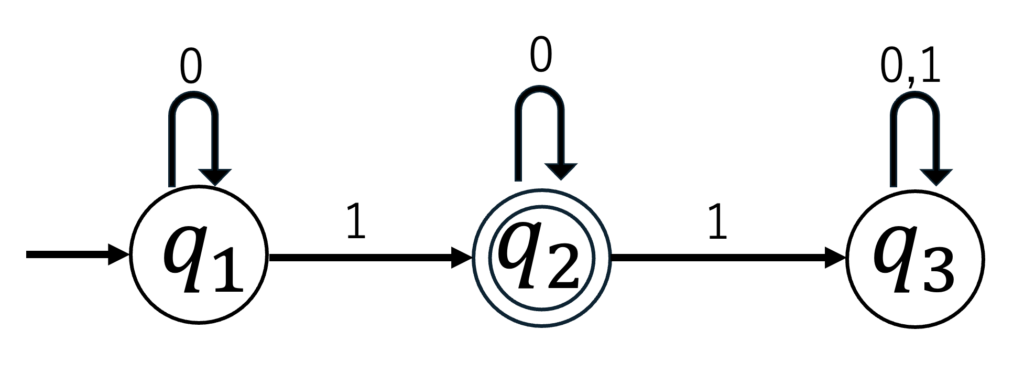
丸の中にある$q_1、q_2、q_3$は状態を表します。

なにも無い方向から遷移してきている$q_1$を初期状態と言い、文字列が入力された時にはこの初期状態の部分から始まります。

そして真ん中の$q_2$のように二重丸で示される状態が受理状態です。

文字を読み終わった時に受理状態、つまり図1においては$q_2$にいれば出力は受理となります。

反対に$q_1、q_3$にいた場合は拒否となります。

実際に例を見てみましょう。

それでは図1の有限オートマトン$M_1$に01という文字列が渡された場合を考えていきましょう。

文字は入力された文字列の左から順に1つずつ処理されます。

よって01の一番左の0から処理されます。

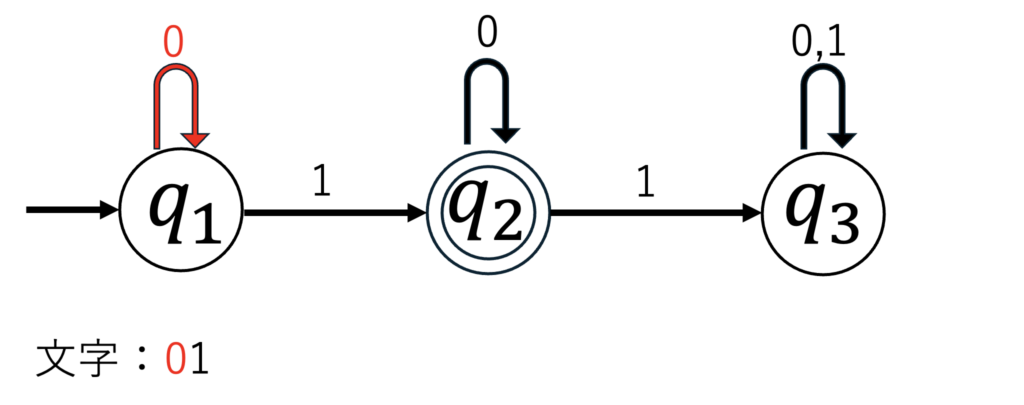
状態遷移図から$q_1$の状態の時、0が読み出されると$q_1$から$q_1$へと遷移します。

次に２番目の1が読み出されると以下の図のようになります。

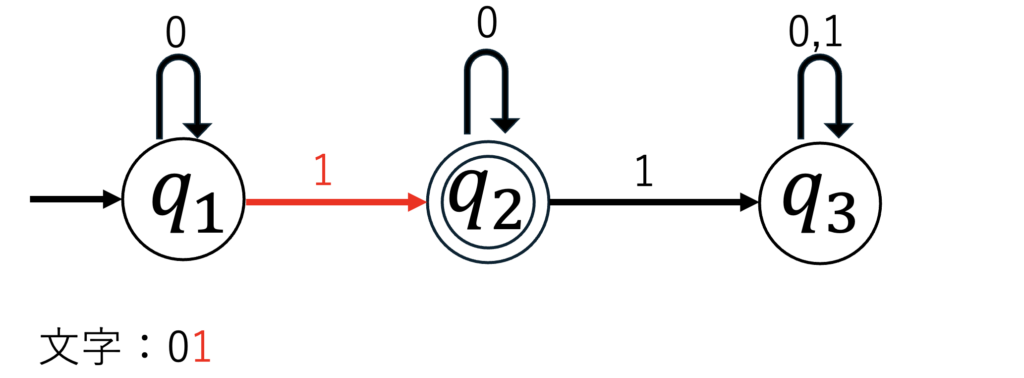
状態は$q_1$から$q_2$へと遷移します。

ここで文字列は2つなので全て読み終えたことになります。

この時$q_2$の状態にいると思います。

$q_2$は受理状態なので、文字列01は受理となります。

続いて、図1の有限オートマトン$M_1$に011という文字列が渡された場合を考えていきましょう。

先程と同様に文字列の左側の0から読み出します。

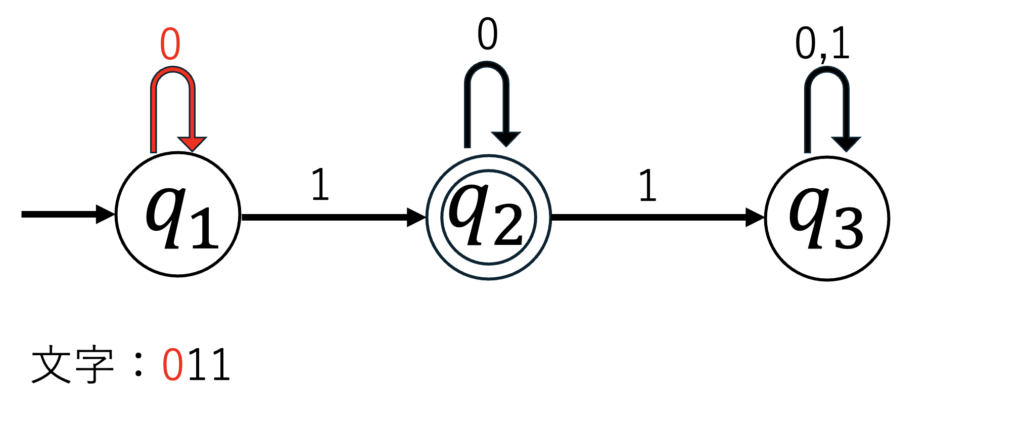
図から分かる通り$q_1$から$q_1$に遷移しました。

続いて２番目の1を読み出します。

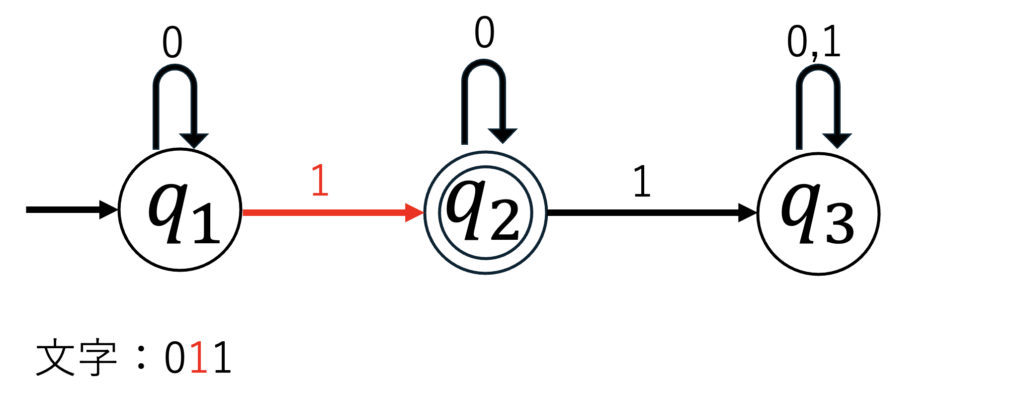
すると、$q_1$から$q_2$へと遷移しました。

続いて最後の1を読み出します。

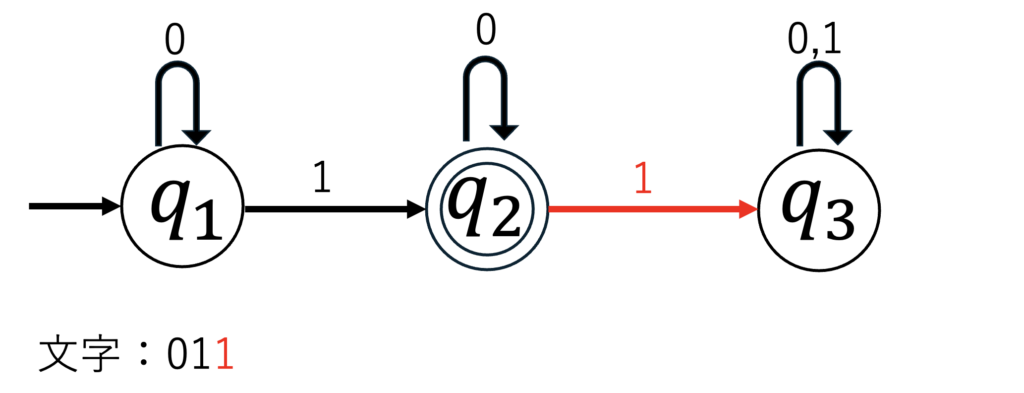
図から$q_2$から$q_3$に遷移したと分かります。

ここで文字列は全て読み出したので現在の状態を確認します。

この時$q_3$の状態にいると思います。

$q_3$は受理状態では無いので文字列011は拒否となります。

ここまでで分かった方もいるかもしれませんが、このオートマトン$M_1$は入力に1が１つだけ含まれる時のみ受理して、1が入っていないか2つ以上入っているものは拒否します。

上記まででは状態遷移図を用いていましたが実際の定義については以下のようになります。

有限オートマトンMは以下の5個組により定義される。
$$
M=(Q,\Sigma ,\delta , q_0,F)
$$
また、この時

$Q$	状態(有限集合)
$\Sigma$	アルファベット(入力文字の有限集合)
$\delta : Q\times\Sigma\rightarrow Q$	遷移関数
$q_0\in Q$	初期状態
$F\subseteq Q$	受理状態の集合

実際に以下の遷移図から考えていきましょう。

これは、先ほどまでの例と同じ図です。

定義に当てはめてみると以下のようになります。

$$
M_1=(Q,\Sigma ,\delta , q_1,F)
$$

$Q=${$q_1,q_2,q_3$}
$\Sigma =${$0,1$}
$\delta =\begin{array}{|c|cc|} \hline現状態& 0 & 1 \\ \hline q_1 & q_1 & q_2 \\ q_2 & q_2 & q_3 \\ q_3 & q_3 & q_3 \\ \hline\end{array} $
$F=${$q_2$}

ここで、有限オートマトン$M_1$が認識する全ての文字列を$A$とするとき$L(M_1)=A$のように書きます。

この時に上記までの例からAは1を一つのみ含む時に認識するので

$$
A=\{ \omega\in \{ 0,1\} | ωに含まれる1の数がちょうど1である\}
$$

と書きます。